Benford’s Law, Part 2

In a prior blog post we showed Benford’s Law in action at Lowe’s.  There we indicated that a popular use of Benford’s Law is to flag potentially suspect expense reports for a closer look.  So we decided to try it on our own expense report data!

We loaded our data into PowerBI and took advantage of the tool’s integration with R to do our statistical analysis, using the Benford package for R.  Although the integration with R makes PowerBI even more powerful, as is sometimes the case, you may need to jump out to a tool like RStudio to do more in-depth analysis.

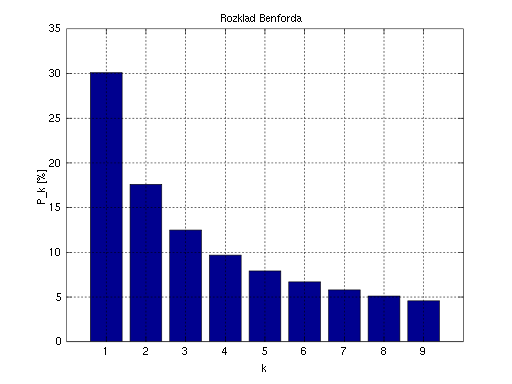
If you read the original blog post and the link to the Wikpedia page, the application of Benford’s Law is about finding deviations from expected patterns of the leading digits in real-life data sets.

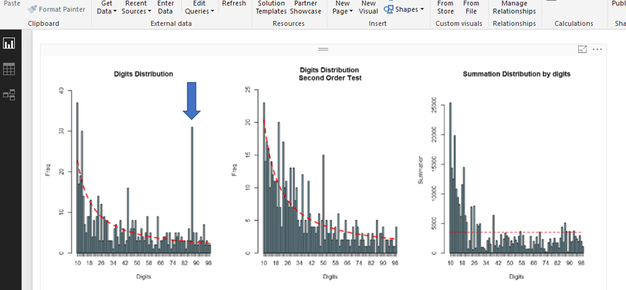
In our case we looked at the first two digits of the dollar amount of the submitted reports.  The Benford package reported that the 5 largest deviations from the expected pattern had the first two digits of 87, 10, 13, 44, and 16.  Graphs returned to PowerBI from R showed those anomalies (the 87, in particular, is highlighted manually).

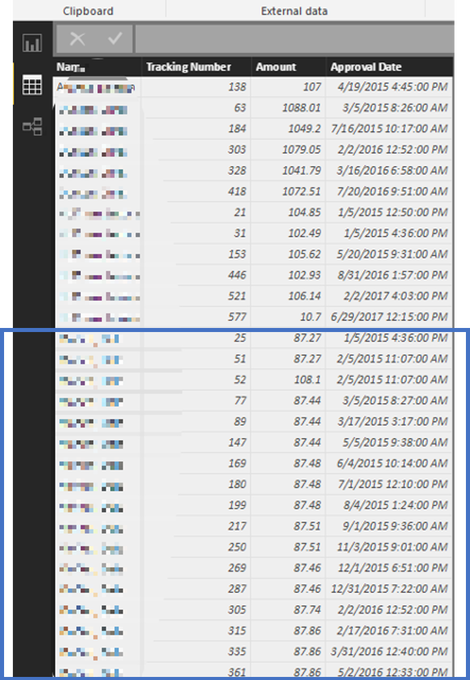
 The ’87’ was an extremely strong anomaly, happening quite frequently.  The Benford package has a getSuspects function that provides the individual data entries that are anomalous.  For us, it produced 68 records to examine (the following picture shows that table, with the individual names pixelated).

 Of those 68, twenty-six of them had the dollar amounts of $87, with some variation of the cents amounts.  All of the reports were submitted by “Jane.” What was Jane up to?  Jane works remotely and it turns out these were her monthly submissions of her reimbursable internet connection.

Of course we don’t really suspect any of our employees, and a check of the remainder of the “suspect records” showed no wrongdoing.

It is usually the case that an anomaly identified by a mathematical model is not truly an anomaly.  But tools like these can process large data sets and identify records a human should look at — for fraud or otherwise.